计算机408算法与数据结构

摘要：静态动态顺序表、单链表、双链表、循环链表、顺序栈、链式栈、顺序循环队列、链式队列

动态顺序表

• 以下增删查操作是索引为index的下标，具体根据要求做改动

  #pragma once
  
  #include <stdio.h>
  #include <stdlib.h>
  
  #define initSize 100
  typedef int ElemType;
  typedef struct {
      ElemType *data;
      int length; //当前的长度
      int maxSize;//最大长度
  } SqlList;
  
  //初始化
  void initList(SqlList &L) {
      L.data = (ElemType *) malloc(initSize * sizeof(ElemType));
      L.length = 0;
      L.maxSize = initSize;
  }
  
  //开辟空间
  void createLength(SqlList &L, int size) {
      ElemType *p = L.data; //备份转移数据
      L.data = (ElemType *) malloc((size + L.maxSize) * sizeof(ElemType));
      // 转移数据
      for (int i = 0; i < L.length; i++) {
          L.data[i] = p[i];
      }
      L.maxSize += size;
      free(p);
  }
  
  //插入
  int insertElem(SqlList &L, int index, ElemType x) {
      //判断合法性
      if (index < 0 || index > L.length)return 0;
      for (int i = L.length; i > index; --i) {
          L.data[i] = L.data[i - 1];
      }
      L.data[index] = x;
      L.length += 1;
      return 1;
  }
  
  //删除
  int deleteElem(SqlList &L, int index, ElemType &e){
      //判断合法性
      if (index < 0 || index > L.length)return 0;
      e = L.data[index];
      for (int i = index; i < L.length - 1; ++i) {
          L.data[i] = L.data[i+1];
      }
      L.length -= 1;
      return 1;
  }
  
  //获取元素
  ElemType getElem(SqlList L, int index){
      //判断合法性
      if (index < 0 || index > L.length)return 0;
      return L.data[index];
  }
  
  //查找元素,有就返回下标,没有就返回-1
  int findElem(SqlList L, ElemType x){
      for (int i = 0; i < L.length; ++i) {
          if (L.data[i] == x) return i;
      }
      return -1;
  }
  //打印
  void showList(SqlList L){
      for (int i = 0; i < L.length; ++i) {
          printf("%d ", L.data[i]);
      }
      printf("length = %d \n", L.length);
  }
  int main() {
  
      SqlList l;
      ElemType x;
      initList(l);
      for(int i = 0;i<10;i++){
          insertElem(l, i, i);
      }
      showList(l);
      insertElem(l, 5, 999);
      showList(l);
      deleteElem(l,2, x);
      showList(l);
      printf("%d \n", getElem(l, 7));
      printf("find: %d\n", findElem(l,9));
      return 0;
  }

  单链表

  

定义

• 带头节点的

  typedef int ElemType;
  typedef struct Node {
      struct Node *next;
      ElemType data;
  } LNode, *LinkList; //LinkList 和 LNode*是一样的
  
  //带头结点的会更方便，这里是带头节点的
  bool initList(LinkList &l) {
      l = (LNode *) malloc(sizeof(LNode));//LNode*强调的是分配一个节点，也可以l = (LinkList)malloc(sizeof(LNode));
      //判断内存够不够，其实可以不用
      if (l == NULL) return false;
      l->next = NULL;
      return true;
  }

• 插入和删除本质上都是找到前面一个节点

插入操作

• 带头节点的插入

  //在第i个位置插入节点，本质上要找到第i-1个节点，以头节点为第0个节点
  bool insertElem(LinkList &l, int i, ElemType x) {
      if (i < 1)return false;
      LinkList p = l;     //p开始指向头节点l,Lnode* p = l;
      int j = 0;          //j表示当前p指向节点的下标
      while (p != NULL && j < i - 1) {
          p = p->next;
          j++;
      }
      if (p == NULL) return false;//i不合法,i太大，远超过节点个数
  
      //到这里时，p已经到了i-1这个位置,可以开辟一块空间了
      LNode *s = (LNode *) malloc(sizeof(LNode));
      s->data = x;
      s->next = p->next;
      p->next = s;
      return true;
  }

• 如果是不带头节点的

  //不带头节点的插入
  bool insertElemNoH(LinkList &l, int i, ElemType x) {
      if (i < 0)return false;
      //单独处理插入第一个节点的情况
      if (i == 1) {
          LNode *s = (LNode *) malloc(sizeof(LNode));
          s->data = x;
          s->next = l;
          l = s;
          return true;
      }
      //下面操作和带头节点的操作是一样的
      LNode *p = l;
      int j = 1;
      while (p && j < i - 1) {
          p = p->next;
          j++;
      }
      if (!p)return false;
      LNode *s = (LNode *) malloc(sizeof(LNode));
      s->data = x;
      s->next = p->next;
      p->next = s;
      return true;
  }

  前插操作

  //前插操作，在节点p前面插入一个节点，值为x
  //时间复杂度为O(1)
  bool insertPriorNode(LinkList &l, LNode *p, ElemType x) {
      if (!p)return false;
      LNode *s = (LNode *) malloc(sizeof(LNode));
      s->next = p->next;
      s->data = p->data;
      p->next = s;
      p->data = x;
      return true;
  }

• 和上面本质一样，其实是交换数据

  //对于指定节点的前插操作,比如在p节点前插入s节点
  bool insertPNode(LNode *p, LNode *s) {
      if (!p || !s)return false;
      s->next = p->next;
      p->next = s;
      ElemType temp = s->data;
      s->data = p->data;
      p->data = temp;
      return true;
  }

  删除操作

//删除第i个节点,由x带回值
bool deleteElem(LinkList &l, int i, ElemType &x) {
    if (i < 1)return false;
    LNode *p = l;
    int j = 0;//p指向的节点下标
    //找到第i-1个节点
    while (p && j < i - 1) {
        p = p->next;
        j++;
    }
    if (!p)return false;//i不合法
    if (!(p->next))return false;//i-1后面没有节点了
    //现在p指向i-1的位置
    LNode *q = p->next;
    x = q->data;
    p->next = q->next;
    free(q);
    return true;
}

• 删除要注意一个细节

  if (!p)return false;//i不合法
  if (!(p->next))return false;//i-1后面没有节点了

  删除指定节点

  //删除指定的节点
  bool deleteTElem(LNode* p){
      if(!p || !(p->next)) return false;
      LNode *s = p->next;
      p->data = s->data;
      p->next = s->next;
      free(s);
      return true;
  }

• 参考

查找

按位查找

//按位查找，找到第i个
LNode *getElem(LinkList l, int i) {
    if (i < 0) return NULL;
    LNode *p = l;
    int j = 0;//j是p的位置下标
    //让跳出循环时，p落在i的位置
    while (p && j < i) {
        p = p->next;
        j++;
    }
    return p;
}

按值查找

//按值查找
LNode * getElemByValue(LinkList l, ElemType x){
    LNode *p = l->next;
    while (p && p->data != x){
        p = p->next;
    }
    return p;//找到返回该指针，找不到返回NULL
}

求表长

• 这是带头节点的，注意表头不算如长度

//求表的长度
int getLength(LinkList l){
    int len = 0;
    LNode *p = l->next;
    while (p){
        p = p->next;
        len++;
    }
    return len;
}

单链表的建立

• 头插法
• 尾插法

尾插法

//尾插法
LinkList insertNextNode(LinkList &l) {
    int x;
    l = (LNode *) malloc(sizeof(LNode));//建立头节点
    l->next = NULL;//如果从外面传入已经初始化的l，那这里就不用写这初始化2句
    LNode *s, *p = l;
    scanf("%d", &x);
    while (x != 9999) {
        s = (LNode *) malloc(sizeof(LNode));
        s->data = x;
        //s->next = NULL;
        p->next = s;
        p = s;  //永远保持p指向最后一个节点
        scanf("%d", &x);
    }
    p->next = NULL;
    return l;
}

头插法

//头插法
LinkList insertHead(LinkList &l) {
    int x;
    l = (LNode *) malloc(sizeof(LNode));//建立头节点
    l->next = NULL;//如果从外面传入已经初始化的l，那这里就不用写这初始化2句
    LNode *s;//头插法只需要记住头节点就行，所以不用像尾插法多设一个p记录尾节点
    scanf("%d", &x);
    while (x != 9999) {
        s = (LNode *) malloc(sizeof(LNode));
        s->data = x;
        s->next = l->next;
        l->next = s;
        scanf("%d", &x);
    }
    return l;
}

双链表

定义

typedef int ElemType;
typedef struct DNode {
    struct DNode *prior;
    struct DNode *next;
    ElemType data;
} DNode, *DLinklist;

初始化

//初始化
bool initList(DLinklist &l) {
    l = (DLinklist) malloc(sizeof(DNode));
    if (!l) return false; //内存不足，分配失败的情况
    l->next = NULL;
    l->prior = NULL;
    return true;
}

后插

//在p节点后面插入s节点
bool insertNext(DNode *p, DNode *s) {
    if (!p || !s) return false;
    s->next = p->next;
    if (p->next) p->next->prior = s;
    p->next = s;
    s->prior = p;
    return true;
}

前删

//在节点p后面删除节点q
bool deleteNext(DNode *p) {
    if (!p) return false;
    DNode *q = p->next;
    if (!q) return false;
    p->next = q->next;
    if (q->next) q->next->prior = p;
    free(q);
    return true;
}

销毁

//销毁，即每一次都删除头节点的下一个节点
void destroyList(DLinklist &l) {
    //释放各个节点
    while (l->next)
        deleteNext(l);
    free(l);
    l = NULL;
}

双向循环链表

• 更加方便
• 实现比上面简单

顺序栈

// 顺序栈
#pragma once

#include <stdio.h>

#define maxSize 100

// 定义
typedef int ElemType;
typedef struct {
    ElemType data[maxSize];
    int top; //栈顶指针
} SeqStack;

//初始化
void initStack(SeqStack &s) {
    s.top = -1; //假设指向栈顶，所以刚开始没有元素是-1,初始也可以设为0，不过代码相应作出改变
}

//判断空
bool isEmpty(SeqStack s) {
    return s.top == -1;//空就返回true
}

//进栈
bool push(SeqStack &s, ElemType x) {
    if (s.top == maxSize - 1) return false;//已满
    s.data[++s.top] = x;
    return true;
}
//出栈,由x带回
bool pop(SeqStack &s, ElemType &x){
    if (s.top == -1) return false;//栈空
    x = s.data[s.top--];
    return true;
}

// 读取栈顶元素
ElemType getTop(SeqStack s){
    if (s.top == -1) return false;
    return s.data[s.top];
}

链式栈

// 链式栈
#pragma once

#include <stdio.h>
# include <stdlib.h>

#define maxSize 100

// 定义
typedef int ElemType;
typedef struct Node {
    struct Node *next;
    ElemType data;
} LinkNode, *LinkStack;

//初始化,这里是带头节点的
void initStack(LinkStack &s) {
    s = (LinkNode *) malloc(sizeof(LinkNode));
    s->next = NULL;
}


//判断空
bool isEmpty(LinkStack s) {
    return s->next == NULL;//空就返回true
}

//进栈
bool push(LinkStack &s, ElemType x) {
    LinkNode *p = (LinkNode *) malloc(sizeof(LinkNode));
    p->data = x;
    p->next = s->next;
    s->next = p;
    return true;
}

//出栈,由x带回
bool pop(LinkStack &s, ElemType &x) {
    if (s->next == NULL) return false;
    LinkNode *p = s, *q = s->next;
    x = q->data;
    p->next = q->next;
    free(q);
    q = NULL;
    return true;
}

// 读取栈顶元素
ElemType getTop(LinkStack s) {
    if (s->next == NULL) return false;
    return s->next->data;
}

void showData(LinkStack s) {
    LinkNode *p = s->next;
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

int main() {
    LinkStack s = NULL;
    initStack(s);
    //push
    for (int i = 0; i < 10; ++i) {
        push(s, i);
    }
    showData(s);
    //pop
    ElemType x;
    pop(s, x);
    showData(s);
    printf("%d \n", x);
    //get
    printf("%d \n", getTop(s));

    return 0;
}

9 8 7 6 5 4 3 2 1 0
8 7 6 5 4 3 2 1 0
9
8

Process finished with exit code 0

顺序循环队列

• 在判断队空和队满时有3种方法，看教材
• 这里列举其中一种

  #pragma once
  
  #include <stdio.h>
  
  #define maxSize 100
  
  typedef int ElemType;
  typedef struct {
      int rear, front; //front指向队头第一个，rear指向队尾的下一个
      ElemType data[maxSize];
  } SeqQueue;
  
  //初始化
  void initQueue(SeqQueue &q) {
      q.front = q.rear = 0;
  }
  
  //判断空
  bool isEmpty(SeqQueue q) {
      return q.rear == q.front;
  }
  
  //入队
  bool enQueue(SeqQueue &q, ElemType x) {
      if ((q.rear + 1) % maxSize == q.front) return false; //已满的情况
      q.data[q.rear] = x;
      q.rear %= maxSize;
      return true;
  }
  
  //出队
  bool deQueue(SeqQueue &q, ElemType &x) {
      if (q.rear == q.front) return false;
      x = q.data[q.front];
      q.front = (q.front + 1) % maxSize;
      return true;
  }
  
  //获取队头元素
  ElemType getTop(SeqQueue q) {
      if (q.rear == q.front) return false;
      return q.data[q.front];
  }
  
  //计算对内元素的个数
  int getNum(SeqQueue q){
      return (q.rear + maxSize -q.front) % maxSize;
  }

  链式队列

#pragma once

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct Node {
    ElemType data;
    struct Node *next;
} LinkNode;//强调的是节点

typedef struct {
    LinkNode *front, *rear;
} LinkQueue;//强调的是队列

//初始化
void initQueue(LinkQueue &q) {
    q.front = q.rear = (LinkNode *) malloc(sizeof(LinkNode));
    q.front->next = NULL;
}

//判断空
bool isEmpty(LinkQueue q) {
    return q.front == q.rear; //或者写q.front->next == NULL;
}

//入队（带头结点的）
void enQueue(LinkQueue &q, ElemType x) {
    LinkNode *p = (LinkNode *) malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    q.rear->next = p;
    q.rear = p;
}

//如果是无头节点的入队，需要判断处理一下对头
void enQueueNoHead(LinkQueue &q, ElemType x) {
    LinkNode *p = (LinkNode *) malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    //空队列的情况
    if (q.front == NULL) {
        q.rear = p;
        q.front = p;
    } else {
        q.rear->next = p;
        q.rear = p;
    }
}

//带头结点的出队
bool deQueue(LinkQueue &q, ElemType &x) {
    if (q.rear == q.front) return false;//队空
    LinkNode *p = q.front->next;
    x = p->data;
    q.front->next = p->next;
    //如果删除的是最后一个元素
    if (p == q.rear)//或者p == NULL
        q.rear == q.front;
    free(p);
    return true;
}

//不带多节点的出队
bool deQueueNoHead(LinkQueue &q, ElemType &x) {
    if (q.front == NULL) return false;
    LinkNode *p = q.front;
    x = p->data;
    q.front = p->next;
    if (q.rear == p) {//或者q.front == NULL
        q.front = NULL;
        q.rear = NULL;
    }
    free(p);
    return true;
}

排序算法

• 算法的稳定性

  比如，排序的数组中有两个数是一样的，那么排序后他们的相对位置如果没有变，那就说明这个排序算法是稳定的，否则是不稳定的

插入排序

• 开始时：

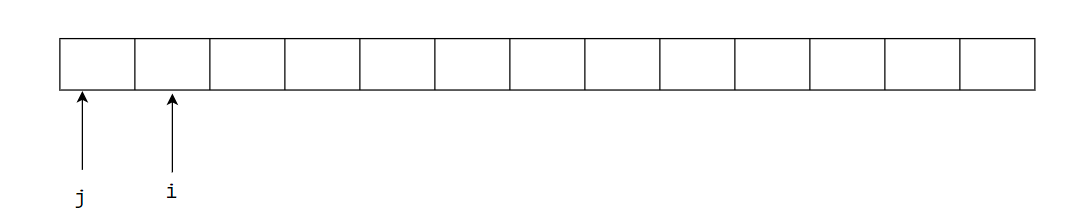
• 比较过程，排序

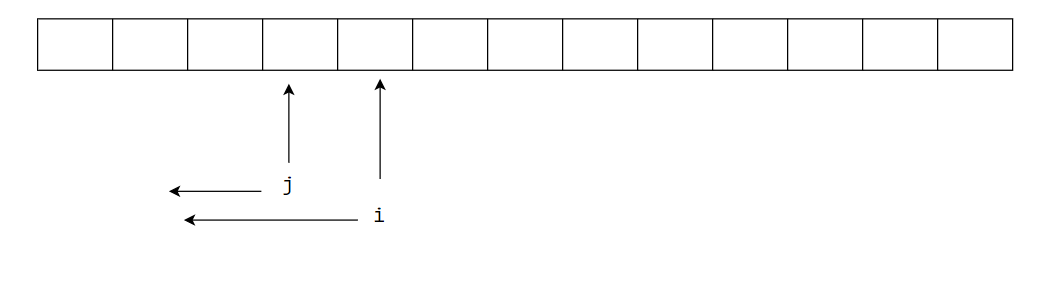
• i前面的元素已经是排序好的了，i所指的元素依次和i前面一个元素比较，如果有比a[i]大的，就要排序了。就先把a[i]保存到temp，然后，temp依次前面的元素比较，如果a[j] > temp,也就是前面的元素仍然大于temp，那么就前面的元素持续依次后移，直到前面所有元素全部比较完为止。

#include <iostream>
using namespace std;

void insertSort(int a[], int n) {
    int i, j, temp;
    for (i = 1; i < n; i++) {
        if (a[i - 1] > a[i]) {
            temp = a[i];
            for (j = i - 1; j >= 0 && a[j] > temp; j--) {
                a[j + 1] = a[j];
            }
            a[j + 1] = temp;
        }
    }
}

int main() {
    int test[] = {3, 2, 7, 6, 9, 9, 1, 0, 54, 23};
    insertSort(test, 10);
    for (int i = 0; i < 10; i++) {
        cout << test[i] << " ";
    }

    return 0;
}

0 1 2 3 6 7 9 9 23 54
Process finished with exit code 0

• 空间复杂度：O(1)
• 平均时间复杂度：O(n^2)，最好是O(n),最坏是O(n^2)
• 算法的稳定性：稳定

冒泡排序

以下按递增顺序来看

• 迭代n趟，每趟依次比较相邻的两个元素，如果a[j]>a[j+1]，就交换彼此
• 经过一趟下来，最右边的元素是最大的
• 优化：
  • 在第二个for的判断中，如果两两元素都没发生交换，那就说明排序已经全部排好了，可以结束排序了，设置标志跳出即可

void bubbleSort(int a[], int n) {
    int i, j, temp;
    for (i = 0; i < n; i++) {
        bool exchange = true;
        for (j = 0; j < n - i - 1; j++) {
            if (a[j] > a[j + 1]) {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                exchange = false;
            }
        }
        if (exchange)return;
    }
}

• 空间复杂度：O(1)

• 时间复杂度:最好O(n),最坏O(n^2),平均是O(n^2)

• 稳定性：稳定

• 每次交换，都需要移动元素次数三次

  temp = a[j];
  a[j] = a[j + 1];
  a[j + 1] = temp;

  • 移动次数和交换次数不同

    交换次数最少是0，最多是n(n-1)/2

选择排序

• 找到最小的和每一趟前面的第一个元素交换
• 外层n-1趟

void chooseSort(int a[], int n) {
    int i, j;
    for (i = 0; i < n-1; i++) {
        int minIndex = i;
        for (j = i+1; j < n; j++) {
            if (a[j] < a[minIndex]) {
                minIndex = j;
            }
        }
        if(minIndex!=i){
            int temp = a[i];
            a[i] = a[minIndex];
            a[minIndex] = temp;
        }
    }
}

• 稳定性：不稳定
• 空间复杂度：O(1)
• 时间复杂度：O(n^2)