Neaya~

笔记、记录、总结

聚类

发表于 更新于 分类于 评论数：
本文字数： 4k 阅读时长 ≈ 4 分钟

摘要：机器学习聚类算法：K-Means、MiniBatchKMeans、DBSCAN算法

聚类算法

K-Means

  • 算法思想：以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果

  • 跟分类相比，没有给定已知标签

  • 用python代码自己实现的Kmeans： https://www.bilibili.com/video/BV1Rt411q7WJ?p=62

    • 注意：sklearn自带的KMeans效果要比自己实现的Kmeans效果好

  • 用sklearn实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
"""
# @Time    :  2020/8/13
# @Author  :  Jimou Chen
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans  # 导入KMeans

# 载入数据
data = np.genfromtxt('kmeans.txt', delimiter=' ')
# 设置k值
k = 4

# 建模
model = KMeans(n_clusters=k)
model.fit(data)

# 各分类的中心点坐标
centers = model.cluster_centers_
print(centers)

# 预测结果
prediction = model.predict(data)
print(prediction)

# 画图
colors = ['or', 'ob', 'og', 'oy']
for i, d in enumerate(data):
    plt.plot(d[0], d[1], colors[prediction[i]])

# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i, center in enumerate(centers):
    plt.plot(center[0], center[1], mark[i], markersize=20)

plt.show()

# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

z = model.predict(np.c_[xx.ravel(), yy.ravel()])  # ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 显示结果
# 画出各个数据点，用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i, d in enumerate(data):
    plt.plot(d[0], d[1], mark[prediction[i]])

# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i, center in enumerate(centers):
    plt.plot(center[0], center[1], mark[i], markersize=20)

plt.show()

1
2
3
4
5
6
7
8
9
[[ 2.6265299   3.10868015]
 [-3.38237045 -2.9473363 ]
 [ 2.80293085 -2.7315146 ]
 [-2.46154315  2.78737555]]
[0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0
 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3 2 1 0 3
 2 1 0 3 2 1]

Process finished with exit code 0


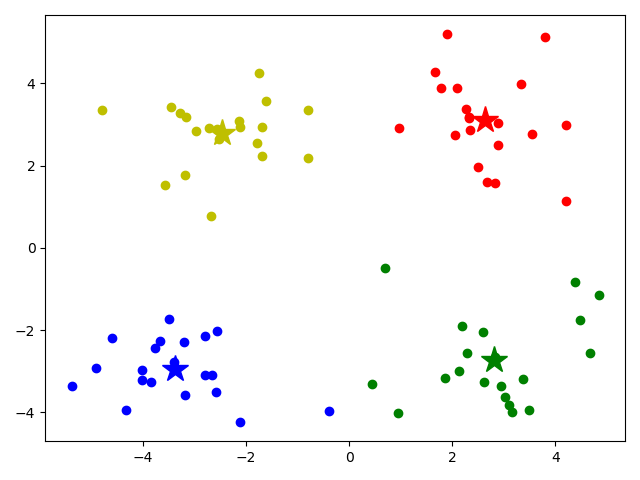
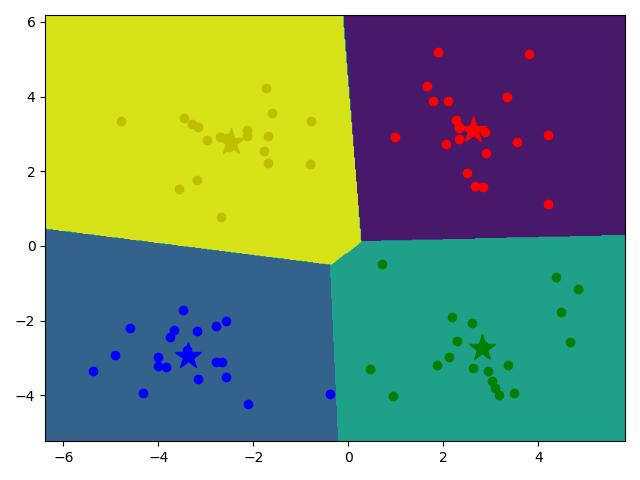
model.fit(data) 只传一个

MiniBatchKMeans模型

  • Mini Batch K-Means算法是K-Means算法的变种
  • 与K均值算法相比，数据的更新是在每一个小的样本集上。Mini Batch K-Means比K-Means有更快的 收敛速度，但同时也降低了聚类的效果，但是在实际项目中却表现得不明显
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
"""
# @Time    :  2020/8/13
# @Author  :  Jimou Chen
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans

'''适用于数据多的情况，但是一般情况还是用KMeans'''

data = np.genfromtxt('kmeans.txt', delimiter=' ')
k = 4

model = MiniBatchKMeans(n_clusters=k)
model.fit(data)

# 分类中心坐标
centers = model.cluster_centers_
print(centers)

# 预测结果
pred_res = model.predict(data)
print(pred_res)

# 画图
colors = ['or', 'ob', 'og', 'oy']
for i, d in enumerate(data):
    plt.plot(d[0], d[1], colors[pred_res[i]])

# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i, center in enumerate(centers):
    plt.plot(center[0], center[1], mark[i], markersize=20)

plt.show()

  • KMeans的4个问题： https://www.bilibili.com/video/BV1Rt411q7WJ?p=65

    • 对k个初始质心的选择比较敏感，容易陷入局部最小值

    • k值的选择是用户指定的，不同的k得到的结果会有挺大的不同

    • 存在局限性，如下面这种非球状的数据分布就搞不定了

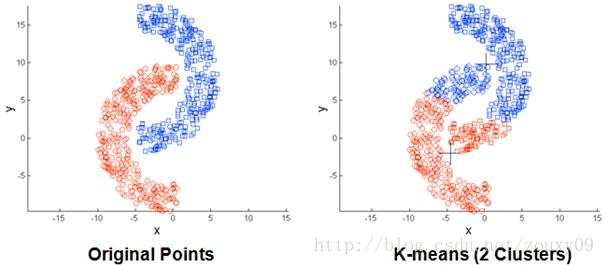
- 数据比较大的时候，收敛会比较慢

DBSCAN

  • 本算法将具有足够高密度的区域划分为簇，并可以发现任何形状的聚类

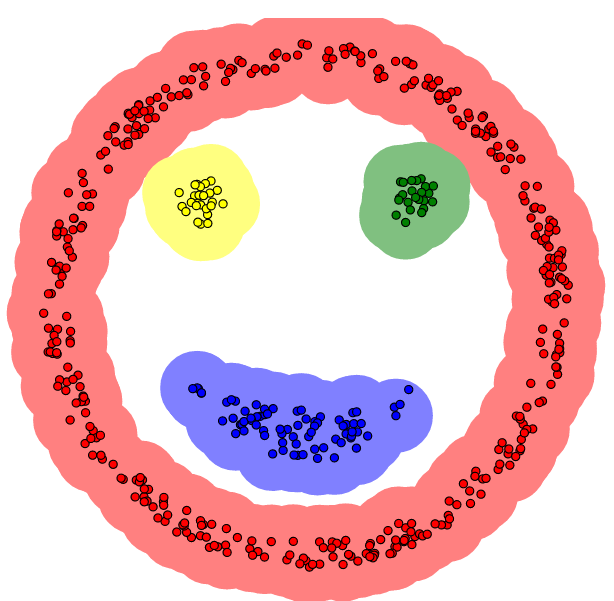
  • 算法思想： https://www.bilibili.com/video/BV1Rt411q7WJ?p=69

  • 缺点：

    • • 当数据量增大时，要求较大的内存支持I/O消耗也很大。
    • • 当空间聚类的密度不均匀、聚类间距差相差很大时，聚类质量较差。

  • DBSCAN和K-MEANS比较：

    • • DBSCAN不需要输入聚类个数。
    • • 聚类簇的形状没有要求。
    • • 可以在需要时输入过滤噪声的参数。

  • 关键参数

    • esp

    • min_point

      即通过调整eps=, min_samples=来找到一个最好的效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
"""
# @Time    :  2020/8/21
# @Author  :  Jimou Chen
"""
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt

data = np.genfromtxt('kmeans.txt', delimiter=' ')
# 建模
# esp距离阈值，min_samples在esp领域里面的样本数
model = DBSCAN(eps=1.5, min_samples=4)
model.fit(data)

# 预测,fit_predict是先拟合后预测，DBSCAN没有predict方法
pred = model.fit_predict(data)
print(pred)  # 预测值为-1的是噪点

# 画出各个数据点
mark = ['or', 'ob', 'og', 'oy', 'ok', 'om']
for i, d in enumerate(data):
    plt.plot(d[0], d[1], mark[pred[i]])
plt.show()

1
2
3
4
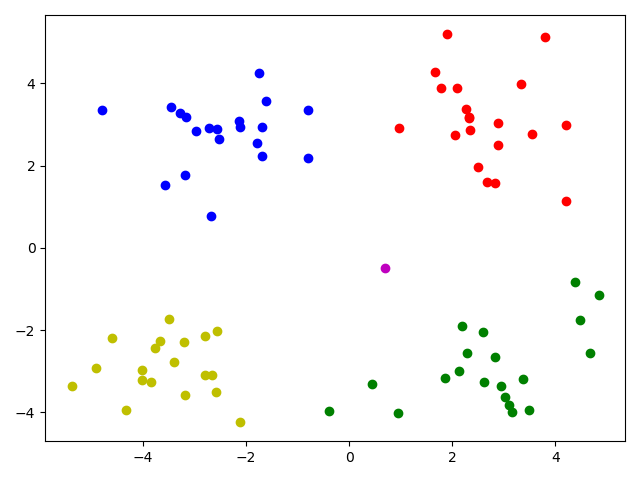
[ 0  1  2  3  0  1  2  3  0  1  2  3  0  1 -1  2  0  1  2  3  0  1  2  3
  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3
  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3  0  1  2  3
  0  1  2  3  0  1  2  3]
  • 预测值是-1 的代表噪点
Welcome to reward