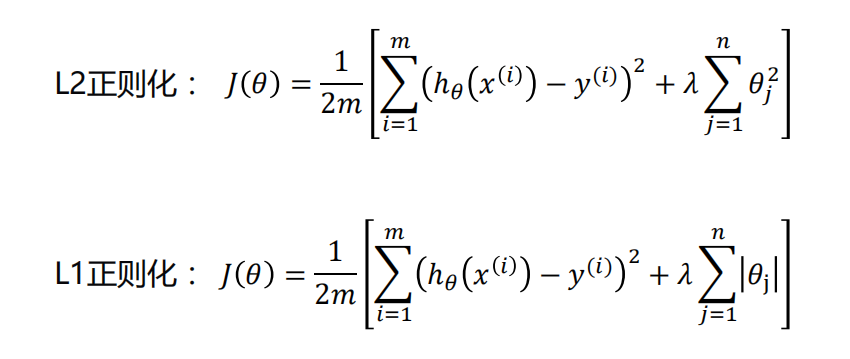回归分析
一元线性回归
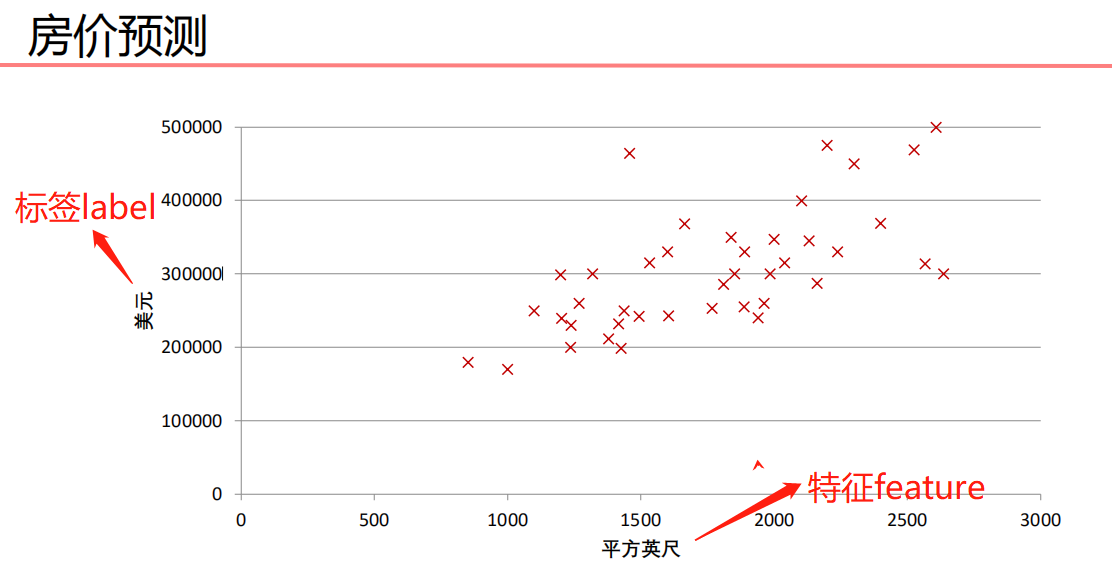
- 被预测的变量是因变量,即输出
- 用来进行预测的变量是自变量,即输入
- 一元线性回归包括一个自变量,一个因变量
- 如果是多元线性回归,那就有多个自变量
代价函数(损失函数)
- m是有m个样本
- 1/2是为了求导时候形式好看一些,其实可有可无
- θ0和θ1是截距和斜率
- 参考: https://www.bilibili.com/video/BV1Rt411q7WJ?p=5
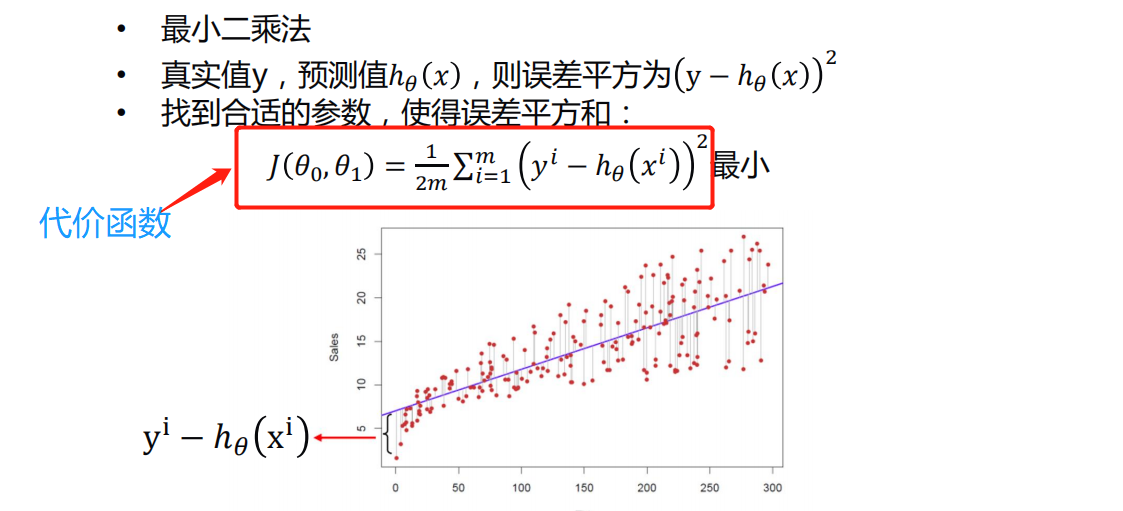
- 代价函数的形式是多种多样的,但是含义是差不多的,上面是一元线性回归的代价函数
梯度下降法
算法思想

- 目的是找到全局最小值
- 缺点,可能找到的是局部最小值,不是全局
- 所以要不断迭代,直到找到全局最小值
1
下面是找到全局最小值
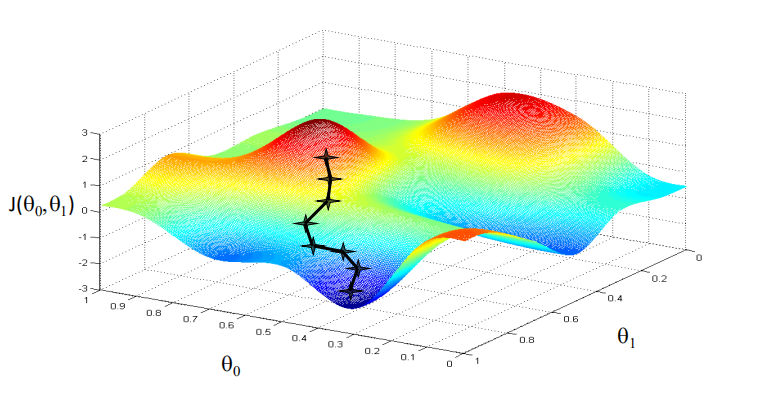
1 | 下面是找到局部最小值 |
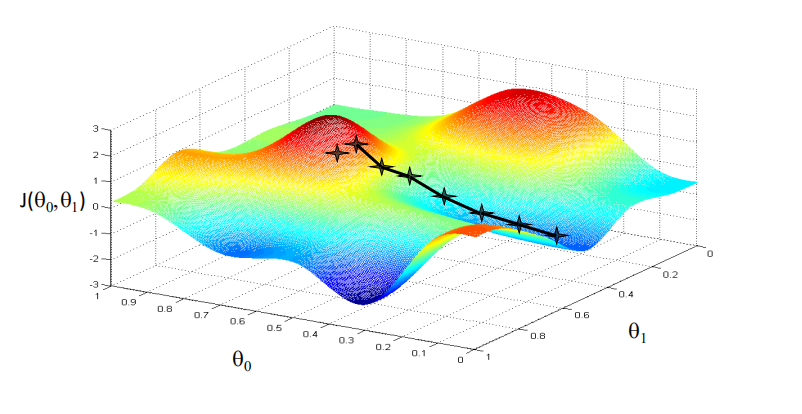
注意

学习率的大小是有讲究的
学习率不能太小,也不能太大,可以多尝试一些值
0.1,0.03,0.01,0.003,0.001,0.0003,0.0001…
线性回归的代价函数是凸函数
用梯度下降法解决一元回归线性问题
参考: https://www.bilibili.com/video/BV1Rt411q7WJ?p=7
1
2# 载入数据
data = np.genfromtxt('data.csv', delimiter=',')genfromtxt是将csv的读取方式是从txt读取进来,因为在csv打开时两列数据是以逗号隔开的,所以用法如上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66"""
# @Time : 2020/8/4
# @Author : Jimou Chen
"""
import numpy as np
import matplotlib.pyplot as plt
# 最小二乘法,返回代价函数的值
def compute_error(b, k, x_data, y_data):
total_error = 0
for i in range(0, len(x_data)):
total_error += (k * x_data[i] + b - y_data[i]) ** 2
return total_error / (2.0 * len(x_data)) # 这里除以2可有可无
# 更新b和k
def get_bk(x_data, y_data, b, k, lr, epochs):
# 计算总数据量
m = len(x_data)
# 循环epochs次
for i in range(epochs):
# 临时变量
b_grad = 0
k_grad = 0
# 计算梯度的总和再求平均
for j in range(0, m):
b_grad += (1 / m) * (k * x_data[j] + b - y_data[j])
k_grad += (1 / m) * (k * x_data[j] + b - y_data[j]) * x_data[j]
# 更新b,k
b = b - lr * b_grad
k = k - lr * k_grad
return b, k
# 载入数据
data = np.genfromtxt('data.csv', delimiter=',')
x_data = data[:, 0] # 所有行都要,但只要第0列
y_data = data[:, 1] # 只要第1列
# 画出分布图
plt.scatter(x_data, y_data)
plt.show()
'''接下来求解回归直线,先求那两个参数'''
# 先定义一些参数
# 设置学习率learning rate,截距,斜率
lr = 0.0001
b = 0
k = 0
# 最大迭代次数
epochs = 50
print('开始时:b = {}, k = {}, error = {}'.format(b, k, compute_error(b, k, x_data, y_data)))
print('正在建模......')
b, k = get_bk(x_data, y_data, b, k, lr, epochs)
print('迭代{}次后, b = {}, k = {}, error = {}'.format(epochs, b, k, compute_error(b, k, x_data, y_data)))
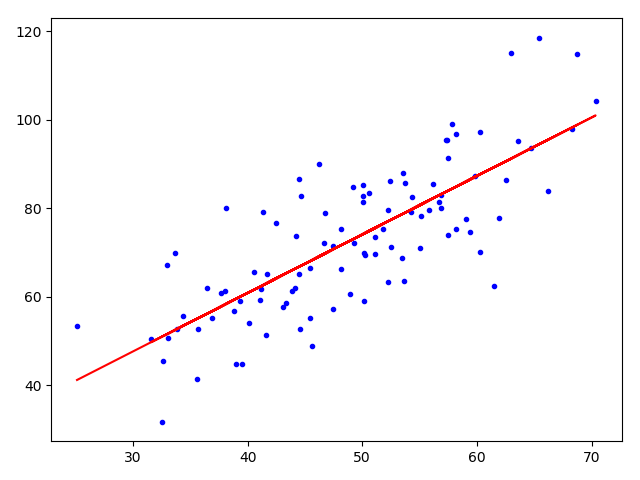
# 画出图像
plt.plot(x_data, y_data, 'b.')
# 画出回归直线
plt.plot(x_data, k * x_data + b, 'r')
plt.show()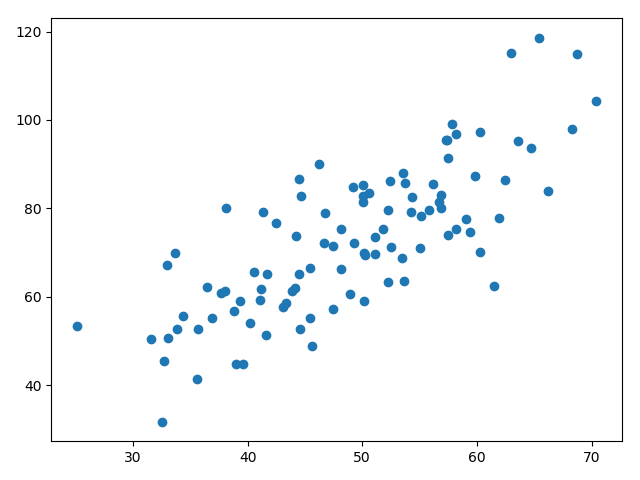

1 | 开始时:b = 0, k = 0, error = 2782.5539172416056 |
- 可以看到error变小了
用sklearn解决一元线性回归
1 | """ |
比起梯度下降法,它直接调用更加方便
注意点是fit的参数格式
必须是二维的
1
2
3# 给他们加个维度变成2维
x_data = data[:, 0, np.newaxis]
y_data = data[:, 1, np.newaxis]model.predict(x_data)预测y_data
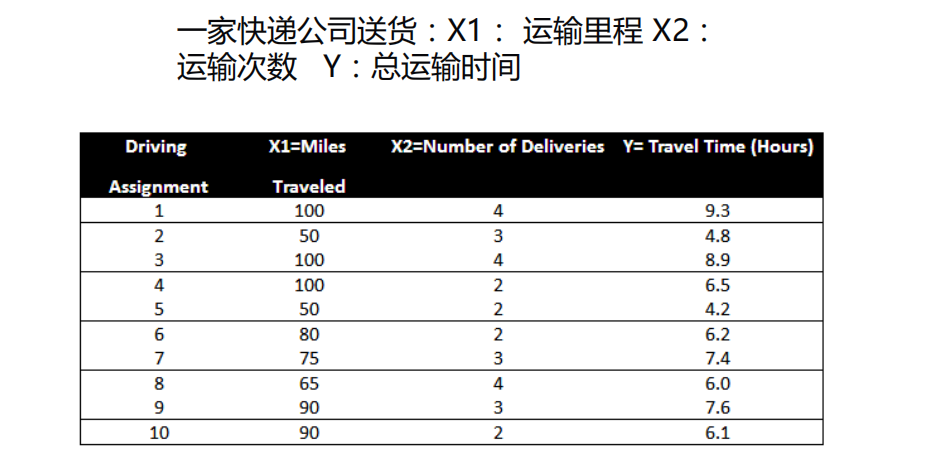
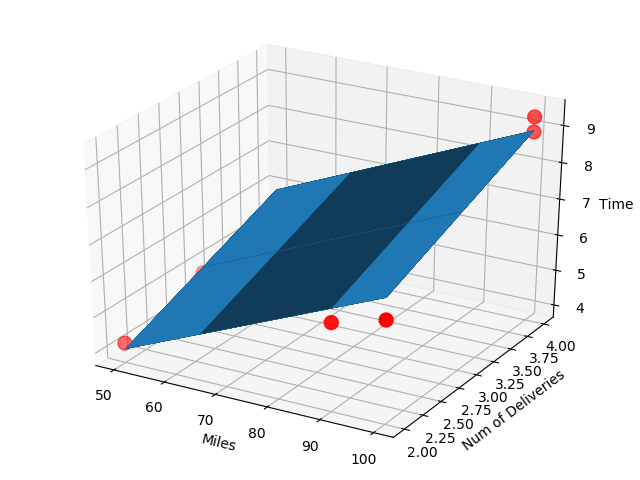
多元线性回归
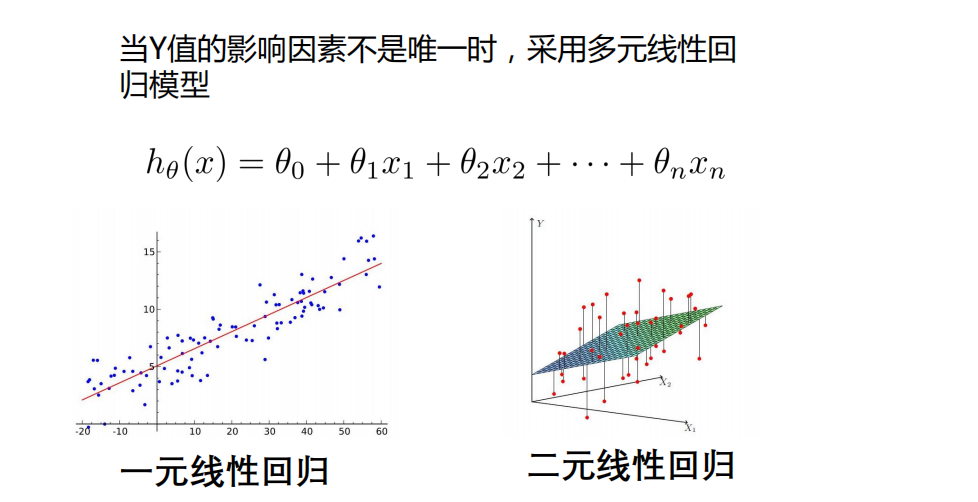
- 做法类似一元
1 | """ |
1 | LinearRegression() |
多项式回归
eg
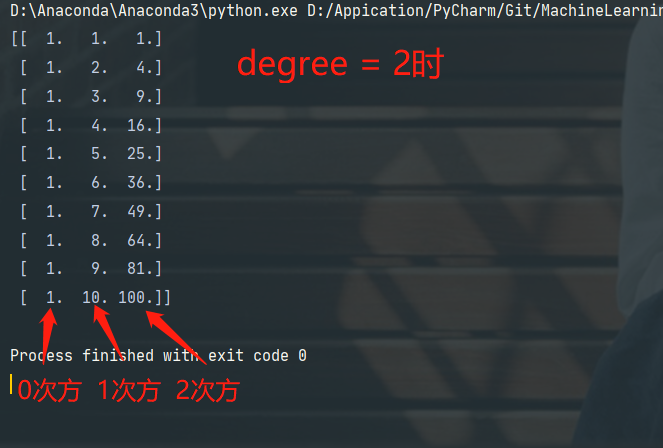
1 | # 定义多项式回归,degree的值可以调节多项式的特征 |
- degree = n,表示n次多项式拟合
- degree = 1时,效果和一元线性回归的效果是一样的
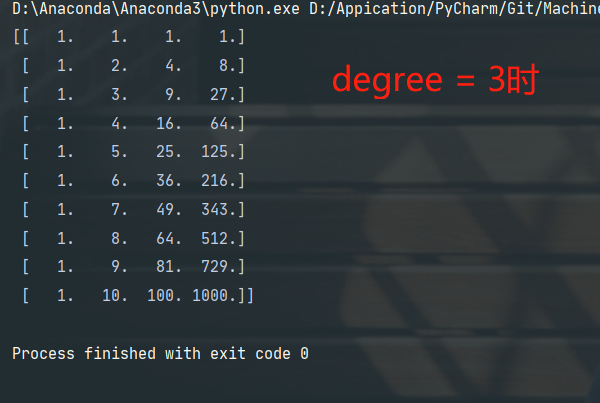
https://www.bilibili.com/video/BV1Rt411q7WJ?p=13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47"""
# @Time : 2020/8/5
# @Author : Jimou Chen
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures # 生成多项式用的
# 读取数据
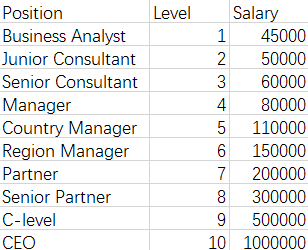
data = np.genfromtxt(r'job.csv', delimiter=',')
x_data = data[1:, 1]
y_data = data[1:, -1]
# plt.scatter(x_data, y_data)
# plt.show()
# 转换为二维数据
x_data = x_data[:, np.newaxis] # 或者x_data = data[1:, 1, np.newaxis]
y_data = y_data[:, np.newaxis] # 或者y_data = data[1:, -1, np.newaxis]
# 建模一元线性回归拟合
# model = LinearRegression()
# model.fit(x_data, y_data)
# 画线性回归线图看看效果
# plt.plot(x_data, y_data, 'b.')
# plt.plot(x_data, model.predict(x_data), 'r')
# plt.show()
# 定义多项式回归,degree的值可以调节多项式的特征
# degree = n,相当于n次方拟合
poly = PolynomialFeatures(degree=5)
# 特征处理
x_poly = poly.fit_transform(x_data)
# print(x_poly)
# 定义回归模型,并拟合
lin_reg = LinearRegression()
lin_reg.fit(x_poly, y_data)
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, lin_reg.predict(x_poly), 'r') # predict 传的是x_poly,是处理后的数据
plt.title('Polynomial Regression')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()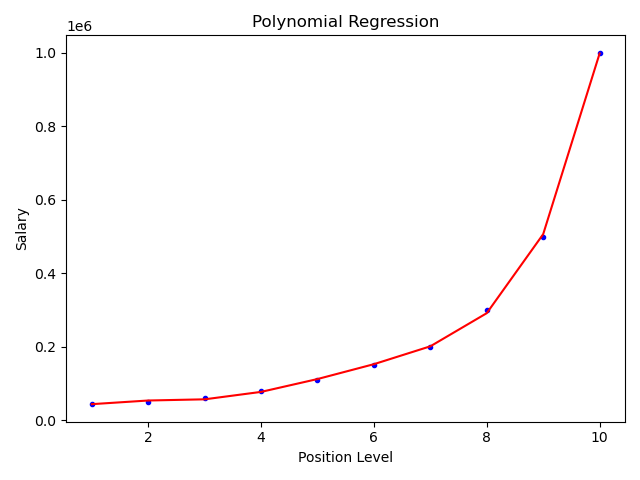
上面是5次方拟合,效果不错
关键步骤如下:
1
2
3
4
5
6
7
8
9# 定义多项式回归,degree的值可以调节多项式的特征
# degree = n,相当于n次方拟合
poly = PolynomialFeatures(degree=5)
# 特征处理
x_poly = poly.fit_transform(x_data)
# print(x_poly)
# 定义回归模型,并拟合
lin_reg = LinearRegression()
lin_reg.fit(x_poly, y_data)如果要画的平滑一些
1
2
3
4
5
6
7
8
9
10
11
12
13'''如果上面画出来10个点的线不够平滑,可以增加自变量,让他平滑一些'''
# 画图
plt.plot(x_data, y_data, 'b.')
x_test = np.linspace(1, 10, 50) # 表示从1到10,之间有50个点
x_test = x_test[:, np.newaxis]
x_poly = poly.fit_transform(x_test) # 一定要处理特征
plt.plot(x_test, lin_reg.predict(x_poly), 'r') # predict 传的是x_poly,是处理后的数据
plt.title('Polynomial Regression')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()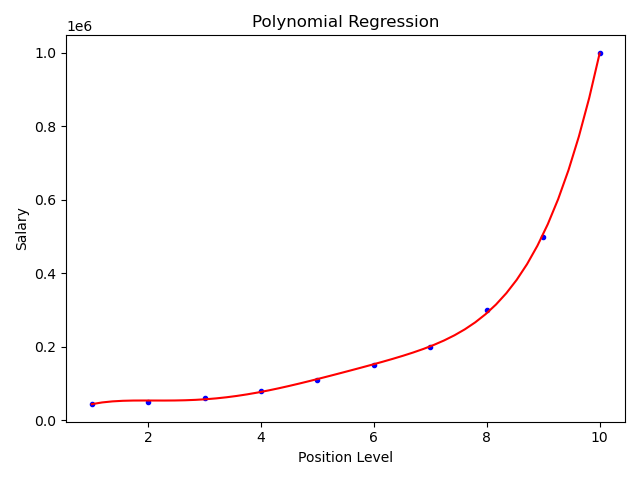
特征缩放
- 用于比如x_data的区间很小,y_data区间很大的情况
数值归一化
数据归一化就是把数据的取值范围处理为0-1或者-1-1 之间。
任意数据转化为0-1之间:
newValue = (oldValue-min)/(max-min)
(1,3,5,7,9)
(1-1)/(9-1)=0
(3-1)/(9-1)=1/4
(5-1)/(9-1)=1/2
(7-1)/(9-1)=3/4
(9-1)/(9-1)=1
任意数据转化为-1-1之间:
newValue = ((oldValue-min)/(max-min)-0.5)*2
均值标准化
x为特征数据,u为数据的平均值,s为数据的方差
newValue = (oldValue-u)/s
(1,3,5,7,9)
u = (1+3+5+7+9)/5=5
s = ((1-5)2+(3-5)2+(5-5)2+(7-5)2+(9-5)2 )/5=8
(1-5)/8=-1/2
(3-5)/8=-1/4
(5-5)/8=0
(7-5)/8=1/4
(9-5)/8=1/2
- 可以看到处理后大多处在[-1/2, 1/2]之间
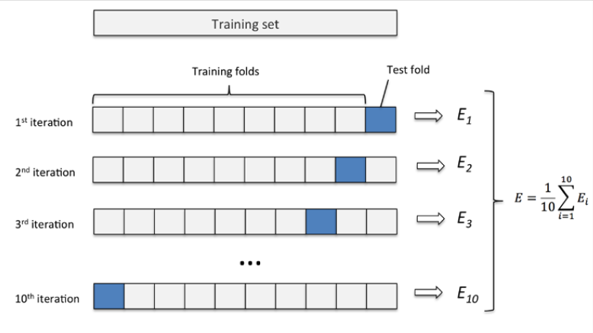
交叉验证法
过拟合
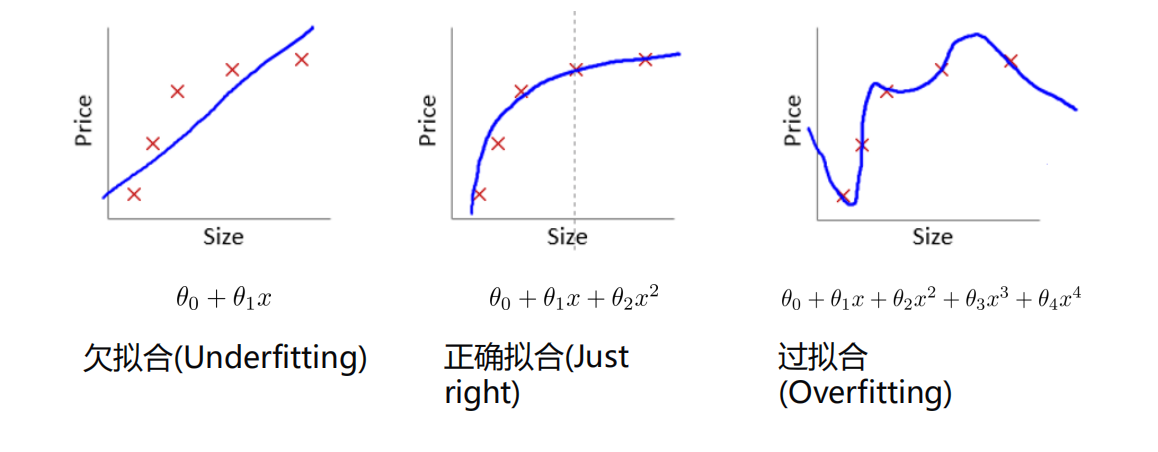
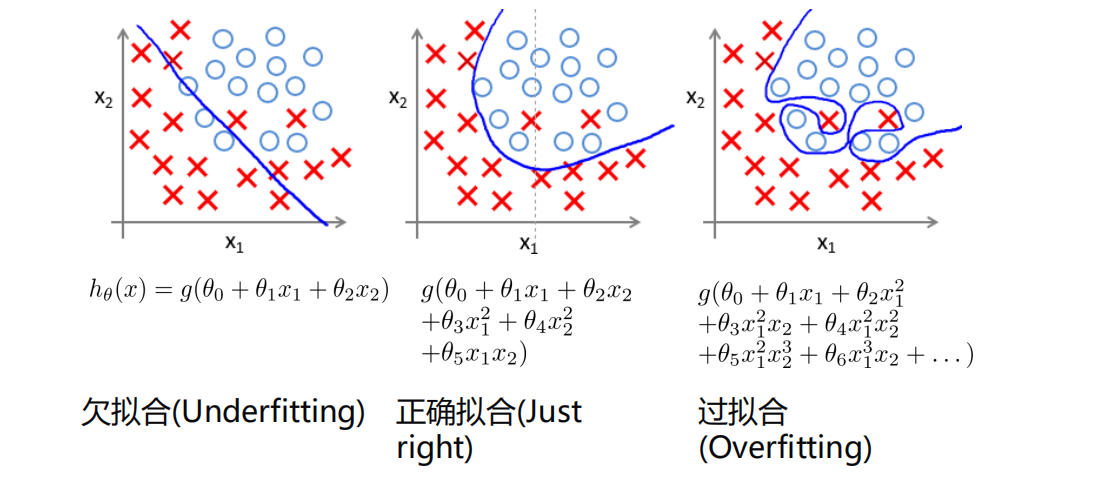
防止过拟合的方法
减少特征
增加数据量
- 在机器学习中,一般数据量越大,拟合的效果越好
正则化
正则化代价函数:
在深度学习还有一些防止过拟合的方法
岭回归
岭回归最早是用来处理特征数多于样本的情况,现在也
用于在估计中加入偏差,从而得到更好的估计。同时也
可以解决多重共线性的问题。岭回归是一种有偏估计。
岭回归代价函数:

- 线性回归标准方程法:
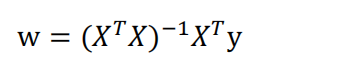
- 岭回归求解:
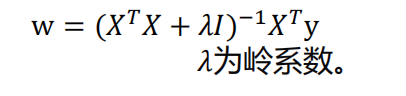
选择𝜆值,使到:
1.各回归系数的岭估计基本稳定。
2.残差平方和增大不太多。
1 | """ |
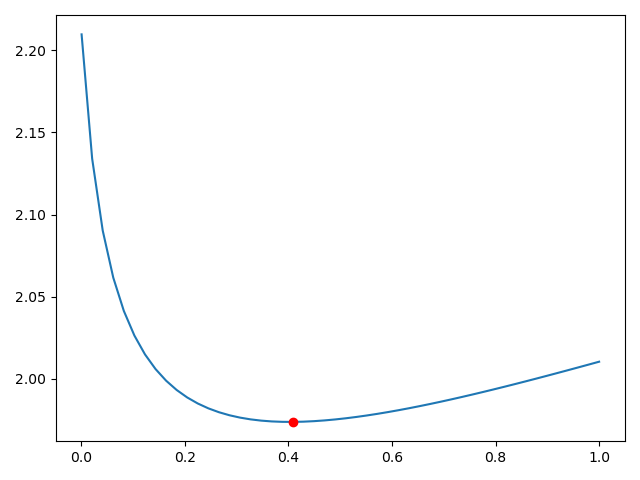
1 | 最好的岭系数 0.40875510204081633 |
关键点
找个岭系数λ范围区间:alphas_test = np.linspace(0.001, 1)
然后把λ范围区间传入,它会自动找到最适合的岭系数,建模拟合,:
model = linear_model.RidgeCV(alphas=alphas_test, store_cv_values=True)
model.fit(x_data, y_data)然后可以预测了:i 表示第i行,
预测第i行:model.predict(x_data[i, np.newaxis])
Lasso回归
- Lasso可以使得某些系数为0,为0说明有多重共线性
- 用起来比岭回归方便
1 | """ |
1 | lasso系数: 14.134043936116361 |
- 经测试,model = LassoCV()比不用交叉验证的Lasso()效果要好
- lasso相关系数打印出来有3个是0,说明有三列是具有多重共线性的
弹性网
- 代价函数
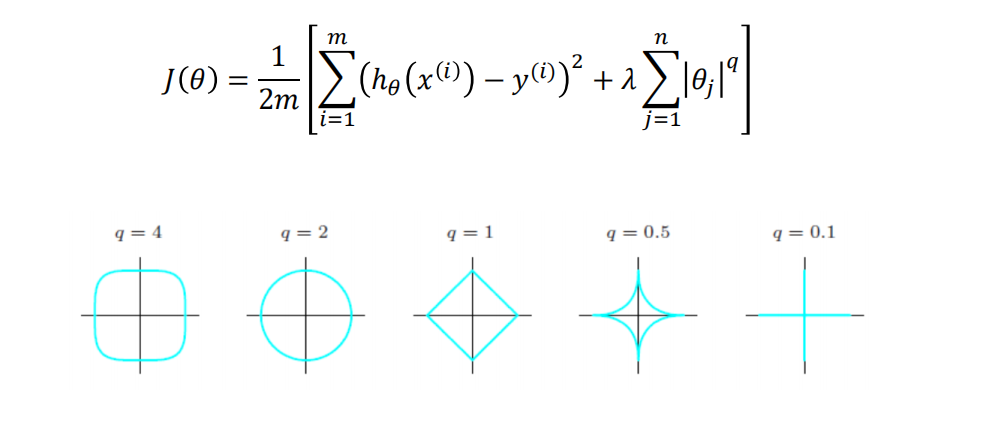
q = 1是Lasso回归
q = 2是岭回归
相对于其他q,Lasso和岭回归效果更好一些,所以用的多
弹性网是Lasso和岭回归的结合
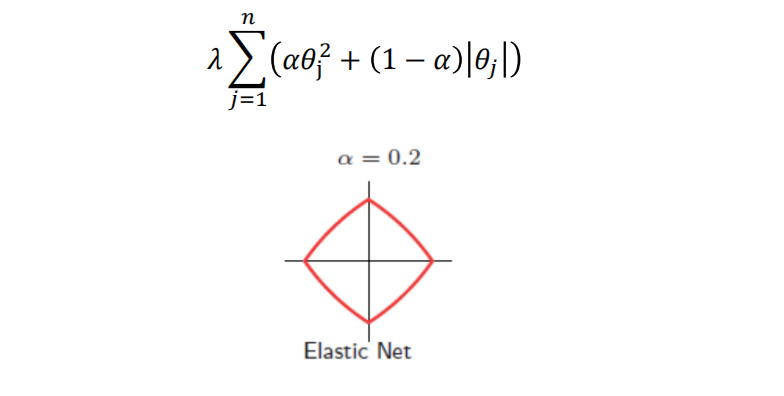
alpha是权重,在sklearn里面会自动调节出一个最适合的alpha系数,即弹性网系数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31"""
# @Time : 2020/8/6
# @Author : Jimou Chen
"""
import numpy as np
from sklearn.linear_model import ElasticNetCV # 导入弹性网模型
import matplotlib.pyplot as plt
data = np.genfromtxt('longley.csv', delimiter=',')
x_data = data[1:, 2:]
y_data = data[1:, 1]
model = ElasticNetCV() # 里面的系数会自动选出最好的,和lasso类似
model.fit(x_data, y_data)
# 预测对比某一行(第2行)
print(model.predict(x_data[2, np.newaxis]))
y_predict = []
for i in range(len(x_data)):
y_predict.append(model.predict(x_data[i, np.newaxis]))
# 画图对比所有的
year = np.linspace(1947, 1962, len(x_data))
plt.plot(year, y_data, 'b.')
plt.plot(year, y_predict, 'r')
plt.show()
print('弹性网系数:', model.alpha_)
print('相关系数:', model.coef_)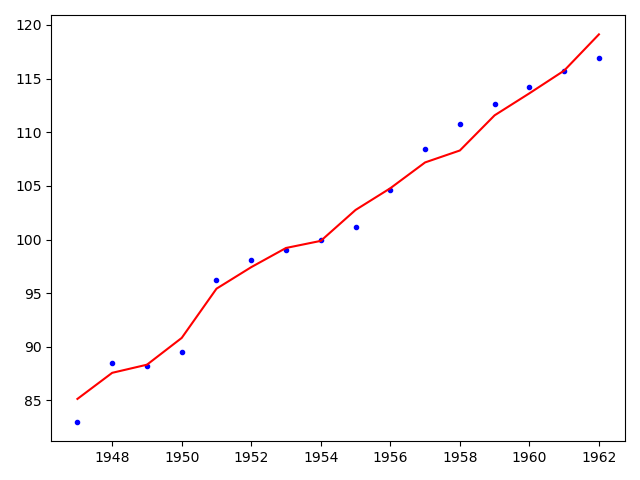
1 | [88.33171474] |
- 效果比岭回归和Lasso回归好,因为结合了两者的优点